Normalized Random Numbers (Bell Curve)

[Baker]

I need normalized random numbers (you know, bell curve ... most of the results are typical with outliers being less common).

Now the best way I've determined to do this, is instead of using one random number and multiply by 3, is to take 3 random numbers and multiply by 1 and add them.

Kind of the board game role playing 3D6 approach:



This was the best way I could think of with the limited math set in QuakeC, but for future use ... is there a "right" way to do this with an extension? The above method works ok for integers, but if you need random floats the above method isn't as useful.

[Lardarse]

[Baker]

[Lardarse]

Double posting for additional insight:

The Box-Muller transform (Wikipedia it) allows you to generate random normals by using two random floats (you will need to filter out random floats that == 1), but it requires:
# either sin() or cos()
# ln() of a number between 0 and 1
# sqrt() (note that this won't result in a complex number because ln(x) is negative if x < 1)
There is a slight variant method (Marsaglia polar method) that doesn't need sin(), but does require more filtering of random numbers.

If implementing an extension, all of those are available in C standard math libraries. However, I beleive that ln() isn't available to the QC yet (there is DP_QC_LOG, but I don't know if it's natural (base e) or base 10).

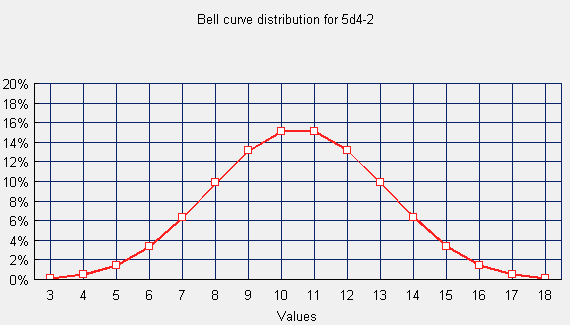
The method I suggest in the last post (essentially, throwing darts at the probability density function) was used to generate . I've not tried this, so I don't know what the rejection rate is, but I suspet it's pretty damn high, and will likely end up with a runaway loop error if implemented fully in QC.

There is one other thing that may provide interesting results: Using randomvec() (either by extension or mathlib), and then using just the x component. It won't go beyond -1 or +1 (so not a true normal deviate), but it will fall in a roughly bellcurve shape. It does however have the advantage of being very well supported...